牛客网算法——名企高频面试题143题(13)
本文共 8503 字,大约阅读时间需要 28 分钟。
反转链表
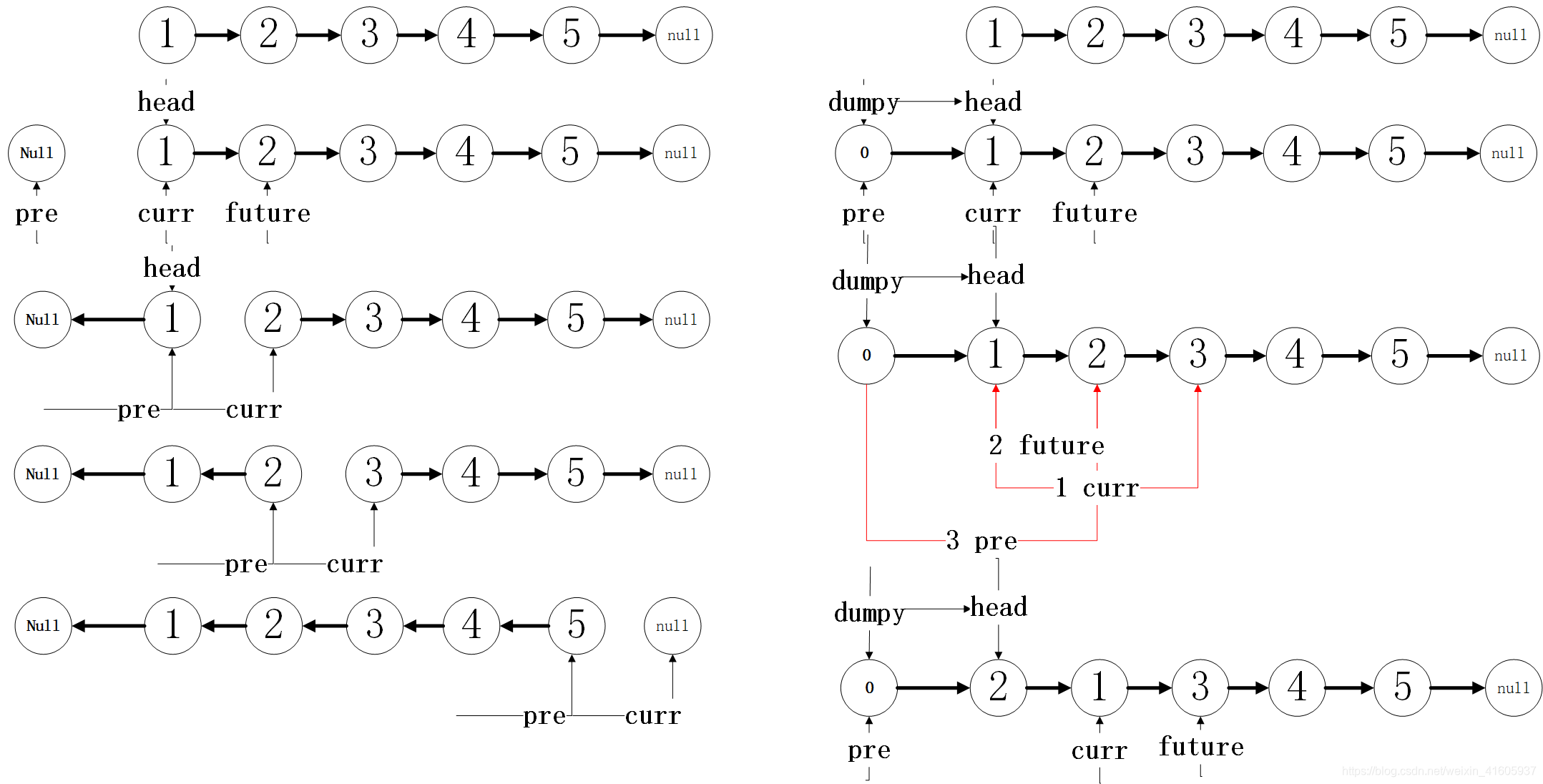
package 复现代码;import org.junit.Test;/** * @Classname 反转链表II * @Description TODO * @Date 2020/12/21 12:56 * @Created by xjl */public class 反转链表II { public class ListNode { int val; ListNode next; public ListNode(int val) { this.val = val; } } public ListNode rever(ListNode head) { if (head == null) { return null; } ListNode pre = null; ListNode curr = head; while (curr != null) { ListNode future = curr.next; curr.next = pre; pre = curr; curr = future; } return pre; } public ListNode rever1(ListNode head) { if (head == null) { return null; } ListNode dumy = new ListNode(0); dumy.next = head; ListNode pre = dumy; ListNode curr = head; while (curr.next != null) { ListNode future = curr.next; curr.next = future.next; future.next = dumy.next; pre.next = future; } return dumy.next; } @Test public void test() { ListNode s1 = new ListNode(1); ListNode s2 = new ListNode(2); ListNode s3 = new ListNode(3); ListNode s4 = new ListNode(4); ListNode s5 = new ListNode(5); s1.next = s2; s2.next = s3; s3.next = s4; s4.next = s5; ListNode res = rever1(s1); while (res != null) { System.out.print(res.val + " "); res = res.next; } }} 链表判断时候有环
package 复现代码;/** * @Classname 判断链表时候有环 * @Description TODO * @Date 2020/12/21 14:38 * @Created by xjl */public class 判断链表时候有环 { public class ListNode { int val; ListNode next; public ListNode(int val) { this.val = val; } } public boolean cycle(ListNode head) { if (head == null) { return false; } ListNode fast = head; ListNode slow = head; while (fast != null && fast.next != null) { fast=fast.next.next; slow=slow.next; if (fast==slow){ return true; } } return false; }} 链表判断环入口
package 复现代码;/** * @Classname 判断环的入口 * @Description TODO * @Date 2020/12/21 14:44 * @Created by xjl */public class 判断环的入口 { public class ListNode { int val; ListNode next; public ListNode(int val) { this.val = val; } } public ListNode test(ListNode head) { if (head == null) { return null; } ListNode fast = head; ListNode slow = head; while (fast != null && fast.next != null) { fast = fast.next.next; slow = slow.next; if (slow == fast) { //表示有环 ListNode start = head; ListNode end = slow; while (start != end) { start = start.next; end = end.next; } return start; } } return null; }} 合并链表
package 复现代码;/** * @Classname 合并链表 * @Description TODO * @Date 2020/12/21 14:53 * @Created by xjl */public class 合并链表 { public class ListNode { int val; ListNode next; public ListNode(int val) { this.val = val; } } /** * @description TODO 链表的都是有序的 * @param: head1 * @param: head2 * @date: 2020/12/21 14:58 * @return: 复现代码.合并链表.ListNode * @author: xjl */ public ListNode merge(ListNode head1, ListNode head2) { if (head1 == null && head2 != null) { return head2; } if (head1 != null && head2 == null) { return head1; } if (head1 == null && head2 == null) { return null; } ListNode dumpy=new ListNode(0); ListNode curr=dumpy; ListNode curr1 = head1; ListNode curr2 = head2; while (curr1 != null && curr2 != null) { if (curr1.val>=curr2.val){ curr.next=curr2; curr2=curr2.next; }else { curr.next=curr1; curr1=curr1.next; } curr=curr.next; } while (curr1!=null){ curr.next=curr1; curr=curr.next; curr1=curr.next; } while (curr2!=null){ curr.next=curr2; curr=curr.next; curr2=curr.next; } return dumpy.next; }} 删除链表中的重复的元素I
package 复现代码;import org.junit.Test;/** * @Classname 删除链表的重复元素 * @Description TODO * @Date 2020/12/21 15:06 * @Created by xjl */public class 删除链表的重复元素 { public class ListNode { int val; ListNode next; public ListNode(int val) { this.val = val; } } public ListNode delete(ListNode head) { if (head == null) { return head; } ListNode curr = head; while (curr.next != null) { if (curr.val == curr.next.val) { curr.next = curr.next.next; } else { curr = curr.next; } } return head; } public ListNode de(ListNode head) { if (head == null) { return null; } ListNode curr = head; while (curr != null && curr.next != null) { ListNode future = curr.next; if (future.val == curr.val) { curr.next = future.next; }else { curr = curr.next; } } return head; } @Test public void test() { ListNode s1 = new ListNode(1); ListNode s2 = new ListNode(1); ListNode s3 = new ListNode(2); ListNode s4 = new ListNode(3); ListNode s5 = new ListNode(3); s1.next = s2; s2.next = s3; s3.next = s4; s4.next = s5; ListNode res = delete(s1); while (res != null) { System.out.print(res.val + " "); res = res.next; } }} 删除链表中的重复的元素II
package 名企高频面试题143;import org.junit.Test;/** * @Classname 链表删除所有重复元素 * @Description TODO * @Date 2020/12/18 10:03 * @Created by xjl */public class 链表删除所有重复元素 { /** * @description TODO 删除的是的链表的重复的元素 * @param: head * @date: 2020/12/18 10:04 * @return: ListNode * @author: xjl */ public ListNode deleteDuplicates(ListNode head) { if (head == null){ return null; } ListNode dumy = new ListNode(0); dumy.next = head; ListNode pre = dumy; ListNode curr = head; while (curr != null && curr.next != null) { ListNode future = curr.next; if (future.val != curr.val) { pre = pre.next; curr = curr.next; } else { while (future != null && future.val == curr.val) { future = future.next; } pre.next = future; curr = future; } } return dumy.next; } public ListNode deleteDuplicates2(ListNode head) { ListNode dummy = new ListNode(-1); dummy.next = head; ListNode prev = dummy; ListNode curr = head; while (curr != null && curr.next != null) { if (curr.val == curr.next.val) { ListNode future = curr.next; while (future != null && future.val == curr.val) { future = future.next; } prev.next = future; curr = future; } else { prev = prev.next; curr = curr.next; } } return dummy.next; } @Test public void test() { ListNode node1 = new ListNode(1); ListNode node2 = new ListNode(1); ListNode node3 = new ListNode(1); ListNode node4 = new ListNode(1); ListNode node5 = new ListNode(1); ListNode node6 = new ListNode(4); ListNode node7 = new ListNode(5); ListNode node8 = new ListNode(6); node1.next = node2; node2.next = node3;// node3.next = node4;// node4.next = node5;// node5.next = node6;// node6.next = node7;// node7.next = node8; ListNode res = deleteDuplicates(node1); while (res != null) { System.out.print(res.val + " "); res = res.next; } } public class ListNode { int val; ListNode next; public ListNode(int val) { this.val = val; } }}
转载地址:http://wqch.baihongyu.com/
你可能感兴趣的文章
mysql生成树形数据_mysql 实现树形的遍历
查看>>
mysql用于检索的关键字_Mysql全文搜索match...against的用法
查看>>
MySQL用得好好的,为什么要转ES?
查看>>
MySql用户以及权限的管理。
查看>>
MySQL用户权限配置:精细控制和远程访问的艺术!------文章最后有惊喜哦。
查看>>
mysql用户管理、常用语句、数据分备份恢复
查看>>
MySQL留疑问:left join时选on还是where?
查看>>
mysql登陆慢问题解决
查看>>
Mysql百万级数据查询优化
查看>>
MySQL的 DDL和DML和DQL的基本语法
查看>>
mysql的 if else , case when then, IFNULL
查看>>
MySQL的10种常用数据类型
查看>>
MySQL的btree索引和hash索引的区别
查看>>
mysql的cast函数
查看>>
MySql的CRUD(增、删、改、查)操作
查看>>
MySQL的DATE_FORMAT()函数将Date转为字符串
查看>>
mysql的decimal与Java的BigDecimal用法
查看>>
MySql的Delete、Truncate、Drop分析
查看>>
MySQL的Geometry数据处理之WKB方案
查看>>
MySQL的Geometry数据处理之WKT方案
查看>>